
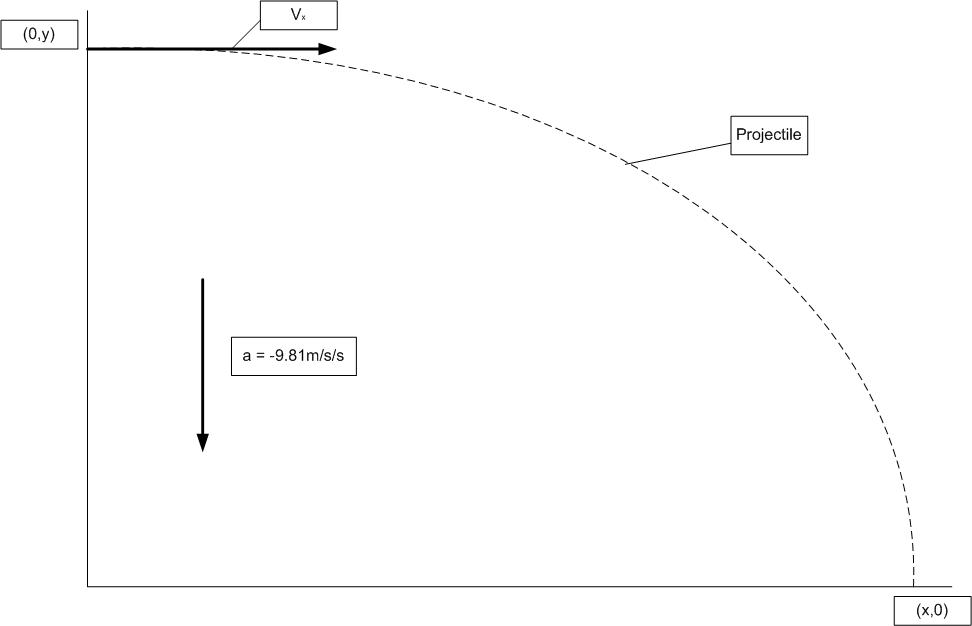
Therefore, the body in a projectile motion has acceleration due to gravity 9.8 m/s 2. These are examples of projectile motion.įor a projectile motion, the gravitational force acting on the body is in the downward direction. A ball that is thrown horizontally from the top of a cliff is also a projectile motion. In this projectile, the body moves along the vertical plane, and the path followed by the body is called a trajectory. A body thrown with an initial velocity at an angle with the horizontal is a projectile motion. For projectile motion, the air resistance acting on the body is neglected and the only force acting on the body is the gravitational force. A body thrown vertically upwards is an example of projectile motion. In Physics, projectile motion is defined as the motion of an object under the influence of gravity. Projectile Motion of a Body Under Gravity Here, we will discuss projectile motion in Physics, which is a two-dimensional motion. The two main examples of two dimensional motion are projectile motion and circular motion. In two-dimensional motion, the body moves along a curved path instead of a straight path. If the motion of the plane is considered along the XY plane, then the x coordinate and y coordinate of the position of the particle changes with time. A more realistic scenario is having the direction of gravity towards a center, which is definitely much harder to derive such an equation, and also you will have to redefine the distance traveled as Δθr, assuming that Earth is a perfect sphere with radius(r).Two-dimensional motion is the motion of a body along a plane. However, this only works for the scenario that the direction of gravity is always one direction that is vertically downwards. Hence the equation can be simplified to s = v^2sin(2θ)/g. Lets remind us about the trigonometry identity sin(2θ) = 2cos(θ)sin(θ). Subsititing the equation, getting s = 2v^2sin(θ)cos(θ)/g. From the equation s = vcos(θ)t, and t = 2vsin(θ)/g. Rearranging the equation for finding t, vsin(θ)/g = t, this is the time it takes to reach its maximum height, so we multiply by 2 to get the total time for it to reach the maximum height and return back to the initial height.


At maximum height, the vertical velocity(vsin(θ)) is reduced to zero, so the equation should give vsin(θ) - gt = 0.
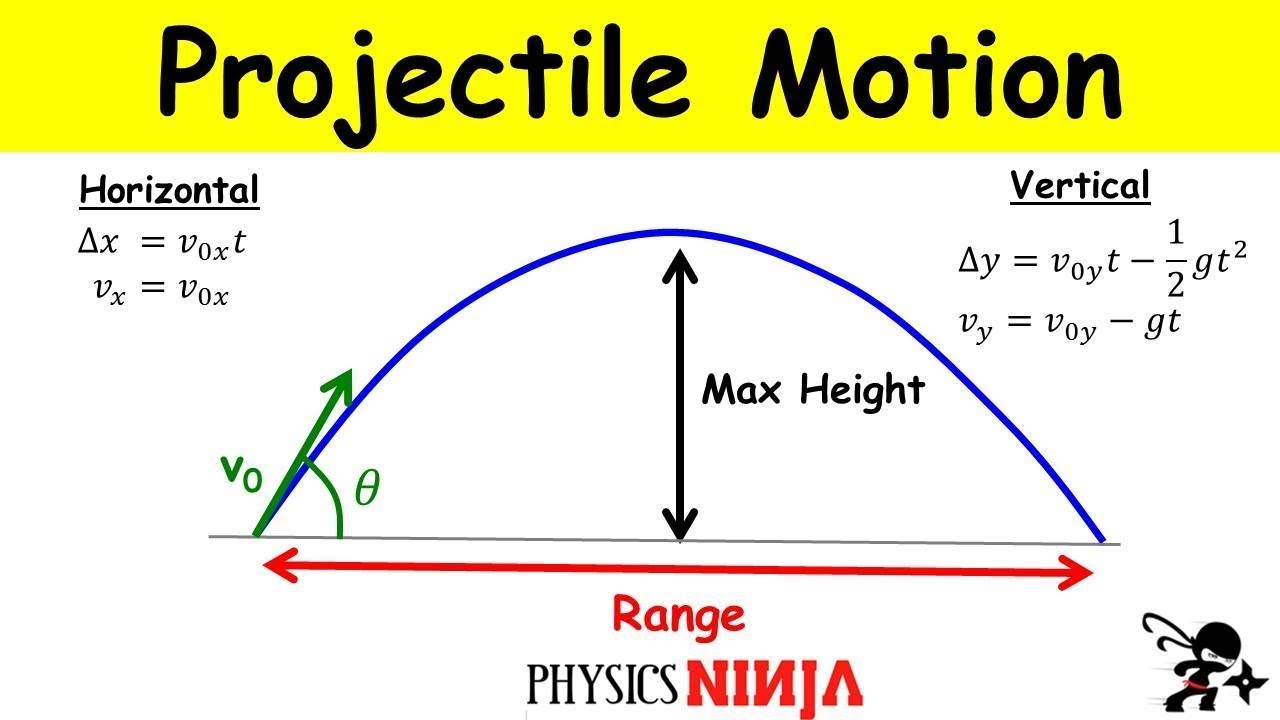
Knowing that the time it takes for the projectile to reach the maximum height from its initial height is the same as the time it takes to fall from the maximum height back to its initial height. So the issue is to find time(t), the time is affected by the vertical component of velocity and the acceleration due to gravity(g). Knowing that the horizontal velocity = vcos(θ), so we can get the horizontal distance(s) = horizontal velocity x time, s = vcos(θ)t.Ģ. Hence the optimal angle of projection for the greatest horizontal distance is 45° because sin(90) = 1, and any other angle will result in a value smaller than 1.ġ. I tried to drive a formula, ending up having the horizontal distance traveled = v^2sin(2θ)/g. For the question of comparing the horizontal distance traveled of different initial angles of projection.


 0 kommentar(er)
0 kommentar(er)
